28. 【存在と形式論理】
![]()
裏路地2回目です。今回は存在文についてやります。前回の内容を踏まえてやっていくのだけど、しっかり復習した?
![]()
まあ、ぼちぼちと。
![]()
不安だな…、まあ多分いけるでしょう!
まずは、この図を見てください!この枠の中には色んな色のついた円と四角があるね。

ソラ、日本語で上の図に関して存在文を4つくらい考えてみて。
![]()
ふむふむ。お安い御用。えーっと。
- 円いものがある。
- 黄色いものがちょうど2つある。
- 赤くて四角いものがある。
- 四角いものが2つ以上ある。
どうでしょう。
![]()
イイ感じ。
さて、存在文で重要なのは「どの範囲での話をしているか」です。
例えば、「黄色いものがちょうど2つある」というのはあの枠内の話なら真だけど、この世界の話なら偽です。
この世界には黄色いものは間違いなく3つ以上あるので、「ちょうど2つ」では無いよね。
この「その文が話題にしている範囲」、つまり「その文が話題にしている対象の集まり」のことを議論領域といいます。
上の場合だと、議論領域は枠内の物々のことになるね。
![]()
議論領域ね。
「あ、鳥がいるよ」っていうのは、私達が見える範囲のものの中に鳥がいるってことであって、世界全体の話じゃないもんね。
![]()
存在文の話に戻そう。日本語での存在文を考えてみたけれど、一般的に存在文というのは
「どんなものがどれだけあるか」
という形式っぽいよね。「どんなものがどれだけあるか」。
![]()
お、「どんなもの」だ。待って!私に言わせて。
存在文ってのはその属性をもつものがどれだけあるかを表してるんじゃないかな。
つまり、「「xはほにゃららだ」という文の x に当てはまるようなものがホニャ個存在する」っていう文なんじゃない?
![]()
前回の内容はちゃんと理解してるみたいだね。
ロジバンでは、形式論理の表現に倣って、次のような構造で存在文を書きます:
「次の文の x を満たすようなものがホニャ個存在する:xはホニャララだ」
つまり、前半部分に「どの自由変項の部分に、いくつのものが当てはまるか」を、後半部分に属性文を書きます。
前半部分の属性文に被さった部分を冠頭(カントウ)と言います。
それから、自由変項に数字を関係付けることを量化すると言います。だから、個数を表す数詞のことを量化詞と呼ぶこともあるよ。
![]()
穴あき文に冠頭をつけることで存在文になるってことか。
![]()
そういうことだね。
それから、形式論理学では、自由変項は量化されると束縛変項になると言うよ。量化詞によって自由を束縛されるってわけだね。
ロジバンでは、自由変項と束縛変項で違う語を使います。
というわけで、実際にロジバンで存在文を言ってみよう!
- da
- 束縛変項その1;量化詞がない場合は su'opa(少なくとも1つ)が想定される。
- de
- 束縛変項その2;量化詞がない場合は su'opa(少なくとも1つ)が想定される。
- di
- 束縛変項その3;量化詞がない場合は su'opa(少なくとも1つ)が想定される。
- zo'u
- 冠頭と文の境界を表す。
- su’o (pa) da zo’u da cukla
- 次のxを満たすようなものが少なくとも1つある:xは円い。(= 円いものが(少なくとも1つ)ある。)
- re da zo’u da pelxu
- 次のxを満たすようなものがちょうど2つある:xは黄色い。 (= 黄色いものが2つある。)
- cukla
- x1 は(二次元的に)円い; x1 は円/ディスク
- pelxu
- x1 は黄色
![]()
量化詞は束縛変項の頭につける んだね。{zo’u}が「:」の役目を果たすわけか。てか、ほんとそのまんまだね。
![]()
でしょ? 基本は「PA da zo’u [daを含む文]」です。PA は数詞(量化詞)のことね。
この形を叩き込んだ上で、もう少し色んな表現を見ていこう。
- 次の文をロジバンに訳せ。
- 赤くて四角いものがある。(ヒント:{gi’e}を使うこと)
- 四角いものが2つ以上ある。
束縛変項の範囲を狭める
![]()
この存在文の形式で「すべての○○は~だ」という文(全称文)も表すことができます。量化詞に{ro}を使えばいいのです。
- ro da zo’u da cukla gi’a kurfa
- 次のxを満たすようなものはすべてである:xは円いか、四角だ。 (= すべてが円いか、四角だ。)
- kurfa
- x1 は x2 (頂角)・ x3 (次元/面)の四角形/長方形
議論領域をこの世界全体として、「すべての犬は動物である」と言ってみよう。
![]()
んー、{ro da zo’u da danlu}だと、「すべてのものは動物だ」になっちゃうよね。
![]()
そう。「議論領域のうちの一部分において」と言いたいときは、束縛変項に poi節をつけてその範囲をさらに制限します 。
- ro da poi ke’a gerku (ku’o) zo’u da danlu
- 犬であるようなすべてのものは動物である。
- re da poi ke’a blanu zo’u da cukla
- (議論領域の)青いもののうちで、円いものがちょうど2つある。
- no da poi ke’a xekri zo’u da kurfa
- 黒いもののうちで、四角いものは0個ある(黒いもので、四角いものはない)。
- danlu
- x1 は x2 (種類)の動物
存在文の略記法
![]()
なんか段々文が長くなってきたね…。
![]()
だね。それじゃ、この辺りで、略記法について紹介します。
まず1つ目。冠頭は省略することができます!その場合、量化子やpoi節は文にある束縛変項につけます。
- su’o da zo’u da cukla = su’o da cukla
- 円いものがある。
- re da poi ke’a blanu zo’u da cukla = re da poi ke’a blanu cu cukla
- 青いもののうちで、円いものがちょうど2つある。
![]()
さらにさらに、文中の{PA da poi ke’a broda} は {PA broda}の形で書けます!
- re da poi ke’a blanu cu cukla = re blanu cu cukla
- 青いもののうちで、円いものがちょうど2つある。
- ro da poi ke’a gerku zo’u da danlu = ro gerku cu danlu
- 犬であるようなすべてのものは動物である。
![]()
おお、ここまでくるとかなり簡潔になるね。ちょっとまとめとこ。
- PA da (poi … ku’o) zo’u da ~ = PA da (poi … ku’o) ~
- PA da poi ke’a broda ku’o ~ = PA broda ~
多重量化
![]()
てなわけで、束縛変項が1つの場合の存在文の表現方法を色々と見てきました。
基本は「PA da (poi … ku’o) zo’u da …」です。これだけはしっかり頭に入れておこう。
さて、束縛変項が2つ以上の場合も、基本的には変わりません。冠頭に束縛変項がもう1つ追加されるだけです。
PA1 da (poi ... ku'o) PA2 de (poi ... ku'o) zo'u da ... de ...![]()
ふむふむ…? ん?この場合、どういう意味になるの?
![]()
冠頭にある束縛変項を前から順番に処理していきます!
- pa da re de zo’u da nelci de
- 次の文の x を満たすようなものが1つ存在する:(次の文の y を満たすようなものが2つ存在する: x は y が好きだ。)
- = 次の文の x を満たすようなものが1つ存在する: x には好きなものが2つある。
- nelci
- x1 は x2 が好きだ
![]()
あー、うーん。分かるようなわからないような。
![]()
落ち着いてみていこっか。体系的な理解のために、地道にやってみよう。
存在文というのは、そこに当てはまるようなものが何個ある、というのを表す文だよね。
たとえば、議論領域が A, B, C, D の4人で、A, B が男、C, Dが女だとしよう。その議論領域で、
- re da zo’u da nanmu
- 次のxに当てはまるようなものが2つ存在する:xは男だ。
が真になるかどうかを地道に調べてみよう(直観的には真だとすぐ分かるよね)。
![]()
「地道に」ね。んー。その変項(da)のところに、議論領域のモノを逐一入れて、その真偽を見ていけばいいかな?
![]()
そうだね。da に A, B, C, Dさんをそれぞれ入れてみて、その真偽を確かめればよさそうだよね。
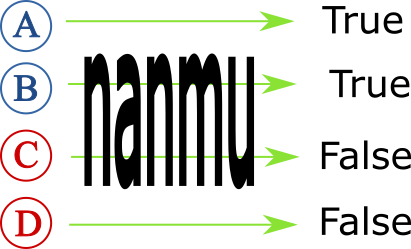
で、ここから、当てはまるものはちょうど2つあるわけだから、{re da zo’u da nanmu}は真だって言えるわけだ!
![]()
うんうん。虱潰しに調べれば、面倒だけど、確実に答えは出るね。
{ro da}なら、こうやって調べて、1つでも偽な文が出たら、元の文も偽。
{su’o da}なら、1つでも真な文が出たら、元の文も真。ってな感じだね。
![]()
だね。束縛変項が2つ以上ある場合も、さっきみたいに虱潰しに調べていけばOKなわけです。
議論領域はさっきと同じで A, B, C, D さんの4人がいるとしよう。
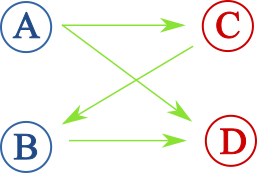
で、AさんはC, Dさんが好き、BさんはDさんだけが好き、CさんはBさんが好き、D さんには好きな人がいないということにしよう。
![]()
いや…この相関図…え…ツラ…
![]()
で、さっきの虱潰し戦法を、冠頭の前から順にやっていきます。つまり、da に A, B, C, D を順に入れていく。
例として、まず da に A を入れてみよう。すると、
- re de zo’u Aさん nelci de
- 次の文の y を満たすようなものが2つ存在する: Aさん は y が好きだ。= Aさんには好きな人が2人いる。
![]()
束縛変項が1つ消えるわけだから、これは今までの文とおんなじだね。直観的にこれは真だって分かる。
![]()
でしょ。まあこれなら直観的に理解できると思います。
が、ここでもあえてド丁寧に虱潰ししていくとしよう。
{re de zo’u Aさん nelci de} の真偽を確かめるためには、やっぱり、de に A, B, C, D さんを順番に入れてみればいいね。
- AさんはAさんが好きだ。→偽
- AさんはBさんが好きだ。→偽
- AさんはCさんが好きだ。→真
- AさんはDさんが好きだ。→真
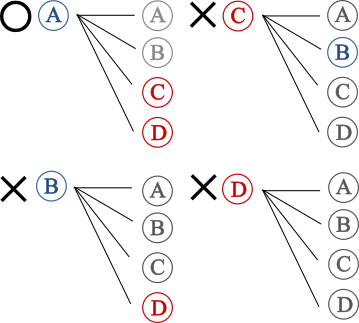
となるので、{re de zo’u Aさん nelci de} は真だね。…というのを、da = B, C, D でもやれば、元の文の真偽が分かるわけです。
![]()
ああ…これで、da に当てはまるのは Aさん1人だけだから、{pa da re de zo’u da nelci de}は真だ!ってことが分かるのね。
すごい冗長だ……けど、確かに原理的にはこうやれば間違いなく文の真偽は分かるね。
でも、「前から順番に処理する」のって意味あるの?なんかどこから処理しても同じ意味な気が…。
![]()
実際にやってみよっか。例として、さっきの文の冠頭を入れ替えてみるよ。
- re de pa da zo’u da nelci de
- 次のyに当てはまるものが2つ存在する:(次のxに当てはまるものが1つ存在する:xはyが好きだ。)
- = 次のyに当てはまるものが2つ存在する:yを好いているものが1つ存在する。
訳文を比較すると、
- 2人の人を好いている人が1人いる。
- 1人の人に好かれている人が2人いる。
となって、これは別に同じ意味ではないよね。
![]()
あー、確かにね。ううむ。一筋縄ではいかないな。
![]()
もう一つ例を挙げるね。
- ro da su’o de zo’u da prami de
- すべてのものがxに当てはまる:(次のyに当てはまるものが存在する:xはyを愛する。)
- = すべてのものがxに当てはまる:xが愛しているものがある。
ここでの議論領域は全人類としようか。これは「すべての人には、それぞれ愛する人がいる」という意味になります。
じゃあ、これの冠頭の2つを入れ替えるとどうなるかというと…
- su’o de ro da zo’u da prami de
- 次のyに当てはまるものが存在する:(すべてのものがxに当てはまる:xはyを愛する。)
- = 次のyに当てはまるものが存在する:すべてのものがyを愛する。
これは「すべての人に愛されるような人がいる」という意味です。明らかに意味が違うよね。
![]()
あー本当だ。ロマンチックな文から、スーパーウルトラアイドルの文みたいになった…。
なるほどよく分かったよ。「前から順番に処理する」のには意味があるんだね。
![]()
もちろん、たまたま入れ替えても意味が変わらないものもあります。が、基本的には変わると思っていたほうがいいね。
ちなみに、さっきやった略記法は束縛変項が2つ以上のときにも使えます。が、1つだけ注意。
冠頭がなくて、束縛変項が複数ある場合は、文の頭の方にある順に処理します。なので、
da broda de = da de zo’u da broda de
となります。処理したい順になるようにSE類で転換する方法もあるけど、基本的には冠頭をつけたほうが読み手に優しいかな。
de da zo’u da broda de = de se broda da ≠ da broda de
![]()
というわけで、チェックテストだ!
- 次の文が真であるとき、この文に関わっている犬の数と男の数の最大と最小を考えよ。
- re gerku cu batci ci nanmu
- ci nanmu cu se batci re gerku
- batci
- x1 は x2 (対象本体)・ x3 (対象箇所)を x4 で噛む
![]()
ふむふむ。とりあえず、2つとも冠頭がある形に直してみるよ。前から処理するから…。
- re da poi gerku ku’o ci de poi nanmu zo’u da batci de
- ci de poi nanmu ku’o re da poi gerku zo’u da batci de
![]()
主文が同じになるように da と de を割り当ててみたよ。そんでだ。えっと、これらの意味は、
- 犬はちょうど2匹おり、そのそれぞれに対して、それが噛むような男が3人いる。
- 男はちょうど3人おり、そのそれぞれに対して、彼を噛むような犬が2匹いる。
だよね。ん?別に変わらないような気も…。
![]()
それぞれの犬が同じ男の人を噛んだとは限らないよね。
![]()
ああ!そうかそうか。
ということは、1の文だと、噛まれた男が最大で(重複なし)6人、最小で(完全に重複)3人いるんだね。で、犬はきっかり2匹と。
で、2の文だと、男はきっかり3人いて、犬は最大で(重複なし)6匹、最小で(完全に重複)2匹だ。表にすると、
| 1. | 2. | |
| 犬 | ちょうど2匹 | 2~6匹 |
| 男 | 3~6人 | 3人 |
かな?
![]()
正解です。1 と 2 の文は、やはり冠頭の da と deを入れ替えた形になってるのだけど、
入れ替えるだけで関わってくるものの数も変動することに注意してね。
![]()
というわけで、裏路地はこれで終わりです。命題、性質、そして、存在文と、ちょっとばかり本質を撫でてみました。
結構難しい内容だったと思うんだけど、どうだった?
![]()
うん、仰る通り難しかったよ…。
でも、こう、今まで学んできたロジバンの知識を駆使して、脳にいい汗かいた感はあるかな。
![]()
お疲れ様でした。実際、この裏路地の話は、ロジバン文法の基盤となっている形式論理学の初歩に足を突っ込んでいます。
![]()
あー、「ロジバンだけどロジバンじゃない」というのはそういうことだったのね。
![]()
何かの機会で形式論理学をすることになったら、役に立つかもしれません。
というわけで、これを以って完クリのエンドロールとするね!
なお、「強くてコンティニュー」では、今のパワーアップした姿で今までの旅路の発展事項を学んでいこう!
True/False Questions
- 冠頭と主文の境目は zo'e によって示す。
- 存在文の真偽は、議論領域によって異なりうる。
- 自由変項を量化すると、その変項は束縛変項と呼ばれる。
- 冠頭は省略することができる。
- pa da re de zo'u da prami de と re de pa da zo'u da prami de は意味が異なる。
- pa de re da zo'u da prami de は冠頭を省略して、 re da prami pa de とすることができる。
-/- answers correct!